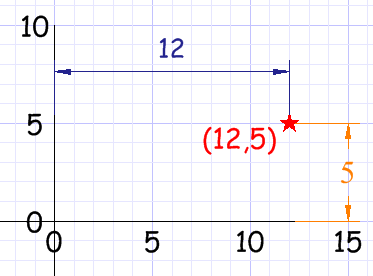
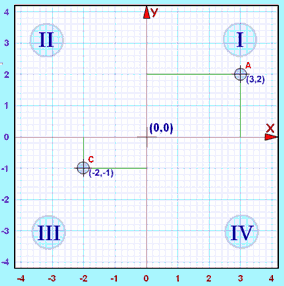
Múltiplos de un número
Actividades de repaso:
Actividades de repaso:
Actividades de repaso:
Criterios de divisibilidad
Mínimo común múltiplo
¿Qué es un "múltiplo común"?
Actividades de repaso:
Máximo común divisor
- Divisores de un número I.
- Divisores de un número II.
- Divisores de un número III.
- Cálculo de divisores I.
- Cálculo de divisores II.
- Cálculo de divisores con la regleta de Cuisenaire.
Números primos y números compuestos.
Un número primo se puede dividir exactamente sólo entre 1 y él mismo.
Un número compuesto se puede dividir exactamente entre otros números además de 1 y él mismo.
(Así que cualquier número entero mayor que 1 es primo o compuesto)
Ejemplos
Número
|
Se puede dividir
exactamente entre |
¿Primo o
compuesto? |
1
|
(1 no es primo ni compuesto)
| |
2
|
1,2
|
Primo
|
3
|
1,3
|
Primo
|
4
|
1,2,4
|
Compuesto
|
5
|
1,5
|
Primo
|
6
|
1,2,3,6
|
Compuesto
|
7
|
1,7
|
Primo
|
8
|
1,2,4,8
|
Compuesto
|
9
|
1,3,9
|
Compuesto
|
10
|
1,2,5,10
|
Compuesto
|
Actividades de repaso:
Criterio de divisibilidad por 2
Un número es divisible por 2, si termina en cero o cifra par.
Criterio de divisibilidad por 3
Un número es divisible por 3, si la suma de sus dígitos es múltiplo de 3.
Criterio de divisibilidad por 5
Un número es divisible por 5, si termina en cero o cinco.
45, 515, 7 525, 230, ...
Criterio de divisibilidad por 9
Un número es divisible por 9, si la suma de sus dígitos es múltiplo de 9.
Actividades de repaso:
- Criterios de divisibilidad I.
- Criterios de divisibilidad II.
- Criterios de divisibilidad III.
- Reglas de divisibilidad.
- Afianzamos lo aprendido.
Mínimo común múltiplo
¿Qué es un "múltiplo común"?
Si tienes dos (o más) números, y miras entre sus múltiplos y encuentras el mismo valor en las dos listas, esos son los múltiplos comunes a los dos números.
Por ejemplo, si escribes los múltiplos de dos números diferentes (digamos 4 y 5) los múltiplos comunes son los que están en las dos listas:
Por ejemplo, si escribes los múltiplos de dos números diferentes (digamos 4 y 5) los múltiplos comunes son los que están en las dos listas:
| Los múltiplos de 4 son 4,8,12,16,20,24,28,32,36,40,44,... |
| Los múltiplos de 5 son 5,10,15,20,25,30,35,40,45,50,... |
| ¿Ves que 20 y 40 aparecen en las dos listas? Entonces, los múltiplos comunes de 4 y 5 son: 20, 40 (y 60, 80, etc. también) |
¿Qué es el "mínimo común múltiplo"?
Es simplemente el más pequeño de los múltiplos comunes distinto de cero.
En el ejemplo anterior, el menor de los múltiplos comunes es 20, así que el mínimo común múltiplo de 4 y 5 es 20.
Calcular el mínimo común múltiploEn el ejemplo anterior, el menor de los múltiplos comunes es 20, así que el mínimo común múltiplo de 4 y 5 es 20.
En realidad es muy fácil de hacer. Sólo escribe los múltiplos de los números hasta que encuentres uno que coincida.
Ejemplo 1: encuentra el mínimo común múltiplo de 3 y 5:
| Los múltiplos de 3 son 3, 6, 9, 15, ..., y los múltiplos de 5 son 5, 10, 15, 20, ..., así: |
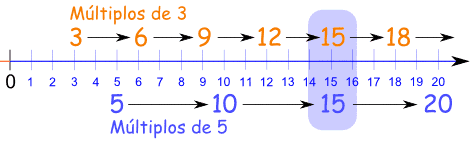 |
| Como puedes ver en esta línea de números, el primer múltiplo que coincide es el 15. Respuesta: 15 |
Y puedes calcular el mínimo común múltiplo de 3 (o más) números.
Ejemplo 2: calcula el mínimo común múltiplo de 4, 6 y 8
Los múltiplos de 4 son: 4, 8, 12, 16, 20, 24, 28, 32, 36, ...
Los múltiplos de 6 son: 6, 12, 18, 24, 30, 36, ... Los múltiplos de 8 son: 8, 16, 24, 32, 40, ....
Entonces 24 es el mínimo común múltiplo de (¡no podemos encontrar uno más pequeño!)
|
Pista: puedes hacer listas más pequeñas de los números más grandes.
Actividades de repaso:
El máximo común divisor de dos o más números es el número, más grande posible, que permite dividir a esos números.
- Para calcularlo. De los números que vayas a sacar el máximo común divisor, se ponen uno debajo del otro, se sacan todos los divisores de los dos números y el máximo que se repita es el máximo común divisor (M.C.D.)
20 : 1, 2, 4, 5, 10 y 20
10 : 1, 2, 4, 5 y 10
M.C.D. (20 y 10) = 10
Actividades de repaso: