La fracción y sus términos. Representación
La fracción se utiliza para representar las partes que se toman de un objeto que ha sido dividido en partes iguales.
Por ejemplo, dividimos una pizza en 8 partes iguales y cogemos tres. Esto se representa por la siguiente fracción:
Los términos de la fracción se denominan: numerador y denominador.
¿Cómo se leen las fracciones? Se leen en función de cuál es su denominador:
1 / 2: un medio
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo
Veamos algunos ejemplos:
Reducción de fracciones a común denominador
Para reducir fracciones a un común denominador tenemos dos métodos:
Método de los productos cruzados de los numeradores.
Para reducir fracciones a común denominador por el método de los productos
cruzados, se multiplican el numerador y el denominador de cada fracción por los
denominadores de las demás.
Método del mínimo común múltiplo.
Reducir fracciones a común denominador es encontrar otras fracciones equivalentes a las originales, de forma que tengan todas igual denominador.
¿Cómo se hace? Seguimos estos pasos:
1) Calculamos el mínimo común múltiplo de los denominadores 2) Como denominador de las nuevas fracciones ponemos el mcm calculado antes. 3)
Como numerador de cada nueva fracción, ponemos el resultado de dividir
el mcm entre el denominador y multiplicar por el numerador.
Ejemplo: Reducir a común denominador las fracciones
1) 
2) 
3) 
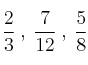
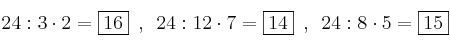
El resultado sería:
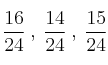
Actividades de repaso:
Comparación de fracciones
Hay tres casos:
Primer caso: dos o más fracciones que tienen igual denominador es mayor la que tiene mayor numerador. Ejemplo:
Segundo caso: dos o más fracciones que tienen igual numerador es mayor la que tiene menor denominador.
Tercer caso: dos o más fracciones con distinto numerador y denominador hay que reducir fracciones a común denominador y a partir de ahí estamos en el primer caso que ya hemos visto.
- fracciones que tienen el mismo denominador;
- fracciones que tienen el mismo numerador;
- fracciones que tienen distinto numerador y denominador.
Primer caso: dos o más fracciones que tienen igual denominador es mayor la que tiene mayor numerador. Ejemplo:
3
|
7
|
----
|
< ----
|
4
|
4
|
La mayor es 7/4.
Segundo caso: dos o más fracciones que tienen igual numerador es mayor la que tiene menor denominador.
5
|
5
|
----
|
< ----
|
4
|
2
|
La mayor es 5/2.
Tercer caso: dos o más fracciones con distinto numerador y denominador hay que reducir fracciones a común denominador y a partir de ahí estamos en el primer caso que ya hemos visto.
Truco: si te cuesta comprender una fracción, recuerda que el denominador son los caramelos que se reparten y el numerador lo que se cogen.
Por ejemplo si te dicen que que es mayor si 3/12 ó 1/6. Piensa que te conviene si coger 3 caramelos de 12 ó 1 caramelo de 6... y verás como intuitivamente te aclaras...
Número mixto
Llamamos número mixto al que tiene una parte entera y otra fraccionaria (una fracción propia –numerador más pequeño que el denominador), por ejemplo:
Actividades de repaso:
Adición y sustracción de fracciones
SUMA Y RESTA DE FRACCIONES CON IGUAL DENOMINADOR
Para sumar o restar fracciones con igual denominador se suman o restan los
numeradores y se deja el mismo denominador.
Veamos un ejemplo:
SUMA Y RESTA DE FRACCIONES CON DISTINTO DENOMINADOR
Pincha sobre la imagen y verás un vídeo explicativo.
Actividades de repaso:
- Suma de fracciones.
- Resta de fracciones.
- Suma y resta con igual denominador.
- Suma con distinto denominador.
- Resta con distinto denominador.
Multiplicación de fracciones
- Multiplicación de un entero por una fracción:
Al multiplicar un número por una fracción estamos calculando la fracción de esa cantidad.
3 / 8 de 320
Se multiplica el numerador por el número y el denominador se deja el mismo.3 x 320 = 960
960 / 8 = 120
Por ejemplo:
En una clase de 30 niños, 2 / 3 nunca juegan al fútbol ¿cuántos son?
(2 / 3) x 30 = (2 x 30) / 3 = 60
60/ 3 = 60 : 3 = 20 niños
División de fracciones
