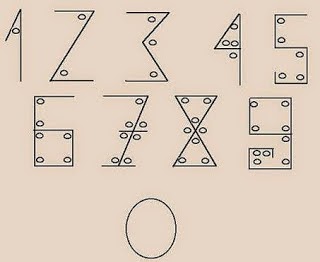
Según ese powerpoint, cada cifra se representa con una forma, trazada a base de rectas, cuyo número de ángulos coincide con el valor numérico de la misma. Así, la representación gráfica del 1 tiene un ángulo, la del 2 consta de dos ángulos, así hasta el 9, del que se muestra también una forma, cercana a la escritura actual, en la que pueden apreciarse nueve ángulos, y por supuesto, el cero, redondo, no tiene ángulos.
¿Será verdad esta hipótesis?
No lo sé pero parece curiosa ¿no?
De hecho, si vamos al libro de Ifrah, resulta que encontramos información sobre el origen de esta “teoría del powerpoint”. Esta es una de las -explicaciones fantásticas a propósito del origen de las cifras “árabes”-, que comenta Ifrah en su libro. Al parecer según una leyenda popular que persiste en Egipto y el norte de África, las cifras “árabes” fueron inventadas por un vidriero geómetra originario del Magreb, el cual imaginó que podría dar a cada una de las nueve cifras significativas una forma evocativa en función del número de ángulos contenidos en el trazado de cada una de ellas.
Parece que fue el director de un museo de Marruecos quien no hace mucho publicó un artículo recuperando esta teoría, poniéndola de moda, en cierto sentido.
Siguiendo el texto de Georges Ifrah, esta teoría también aparece en la obra de un autor francés P. Voizot, de finales del siglo XIX, quien pudo tomarla de un genovés. Además, este francés considera igualmente probable (según su parecer), una explicación por encaje de trazos (el uno es un trazo vertical, el dos se dibujan dos trazos horizontales y al unirlos aparece el dos; el tres son tres trazos horizontales y al unirlos sale el tres; el cuatro serían cuatro trazos; etc). Es lo que Ifrah llama la segunda hipótesis fantástica.